约束优化（constrained optimization）相关理论

概念

对于一个约束优化问题，通常建模为：

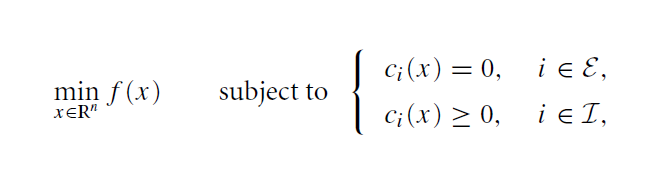
通常 $f(x)$ 是光滑的实值函数。$\mathcal{E}$ 代表等号约束的有限集合，$\mathcal{I}$ 是不等式约束的优先集合。用 $\Omega$ 代表可行域。

紧凑的写法就是： $$ \min_{x\in\Omega} f(x) $$

回顾，对于非约束优化问题的条件：

necessary condition 必要条件：局部极小值点有 一阶导数为零，二阶导数半正定；

必要条件就是解必须满足的条件。

sufficient condition 充分条件：所有点满足一阶导数为零，二阶导数是整数的点是函数的局部极小值点。

充分条件就是：如果x满足该条件，那么x就是解。

局部解：

严格局部解：

隔离局部解：

情况1：一个等号约束

对于这样的问题： $$\min x_1+x_2\ s.t. x_1^2+x_2^2=2 $$

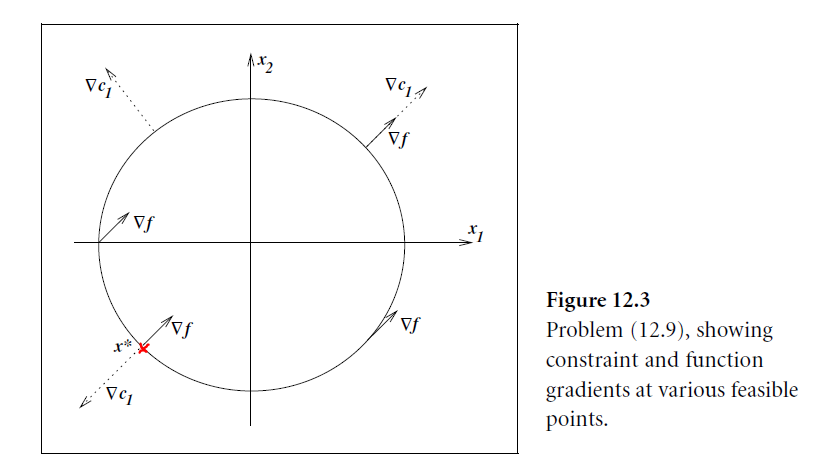
$x^*$ 点（红色）是最优解，可以发现在这个圆上，除了$x^*$ 以外所有的点都可以找到一个路径，减小 $f$ 的同时，保持可行。

同时可以发现，$x^*$ 点（红色）的约束法线 $\nabla c_{1}\left(x^{*}\right)$ 是平行于梯度 $\nabla f(x^*)$ 的，所以存在一个系数使得:

$$\nabla f\left(x^{*}\right)=\lambda_{1}^{*} \nabla c_{1}\left(x^{*}\right)$$

下面使用一节泰勒展开推导上式：

对于 $c_{1}\left(x\right)=0$ , 有一个微小的步长$s$，满足$c_1(x+s)=0$，写为： $$ 0=c_1(x+s)\approx c_1(x)+ \nabla c_1(x)^Ts=\nabla c_1(x)^Ts $$ 所以可以说，如果说微小步长 $s$ 满足 $c_1$ 的可行性，在一阶情况下，满足条件： $$ \nabla c_1(x)^Ts=0 $$ 同样的，对于 $f(x)$ 来说，我们希望步长s使得 $f(x)$ 减小，所以： $$ 0>f(x+s)-f(x)\approx \nabla f(x)^Ts $$ 所以说对于上面两个条件：

1. $\nabla c_1(x)^Ts=0$
2. $0> \nabla f(x)^Ts$

这两个条件满足-->存在微小步长s--->那么就存在一个方向d，$d \approx s/||s||$ 满足上面两个条件：

$\nabla c_1(x)^Td=0$ 并且$0> \nabla f(x)^Td$ 。

反而言之，如果说这个d不存在，那么我们就在x附近找不到比它小的数值，说明x是局部最小。

通过画图可以发现，当$\nabla c(x)$ 和 $\nabla f(x)$ 平行的时候，也就是$\nabla c(x)=\lambda \nabla f(x)$，我们是找不到满足条件的 $d$。

引入拉格朗日函数： $$ \mathcal{L}\left(x, \lambda_{1}\right)=f(x)-\lambda_{1} c_{1}(x) $$ 导数为： $$ \nabla_{x} \mathcal{L}\left(x, \lambda_{1}\right)=\nabla f(x)-\lambda_{1} \nabla c_{1}(x) $$ 若存在乘子 $\lambda_{1}^*$ 使得 $\nabla_{x} \mathcal{L}\left(x, \lambda_{1}\right)=0$，则 $\nabla f(x)=\lambda c(x)$。这样一来，我们可以将等号约束的问题转化为寻找拉格朗日函数的驻点问题。$\lambda$ 为拉格朗日乘子。

显然，$\nabla c(x)=\lambda \nabla f(x)$ 这个条件只能是一个必要条件，不能说是充分条件。

情况2：一个不等号约束

对于这样的不等号约束问题： $$ \min x_1+x_2\ s.t. x_1^2+x_2^2<=2 $$ 将情况1的圆环转化为了一个圆的内部与环。

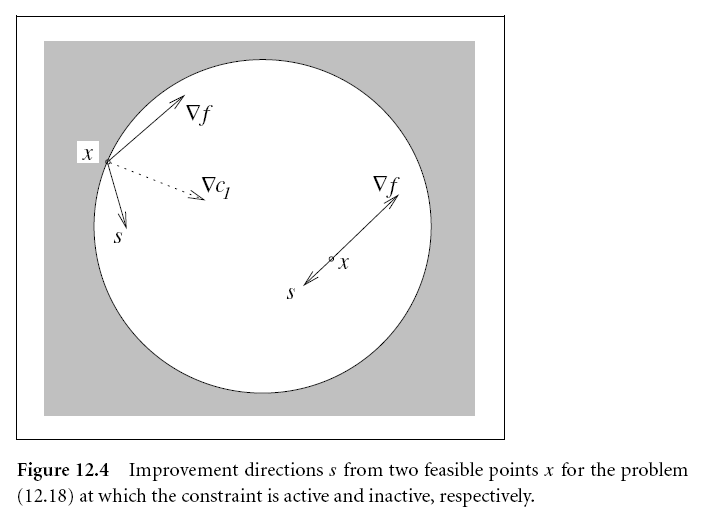
对于这个问题，依旧可以知道$x^*=(-1,-1)^T$，$\lambda =1/2$ 。

对于不等式约束，我们希望x附件比当前c(x)大，或者相等： $$ 0 \geq c(x+s) \approx c(x)+ \nabla c(x)^Ts $$ 所以在一阶情况写为： $$ c(x)+ \nabla c(x)^Ts \geq 0 $$ 第二个条件和情况1一样，写为： $$ 0> \nabla f(x)^Ts $$ 如果说 x严格位于圆的内部，也就是说 c(x)>0。那么任何方向上的步长都能满足$c(x)+ \nabla c(x)^Ts \geq 0$ ，只要它足够短。

如果说x位于圆环上，那么就和情况1讨论的一样。只要 $\nabla c(x)$ 和 $\nabla f(x)$ 不平行，就能找到一个方向d进行搜索。如下图所示，两者不平行，灰色区域都是可以搜索的空间，满足两个条件。

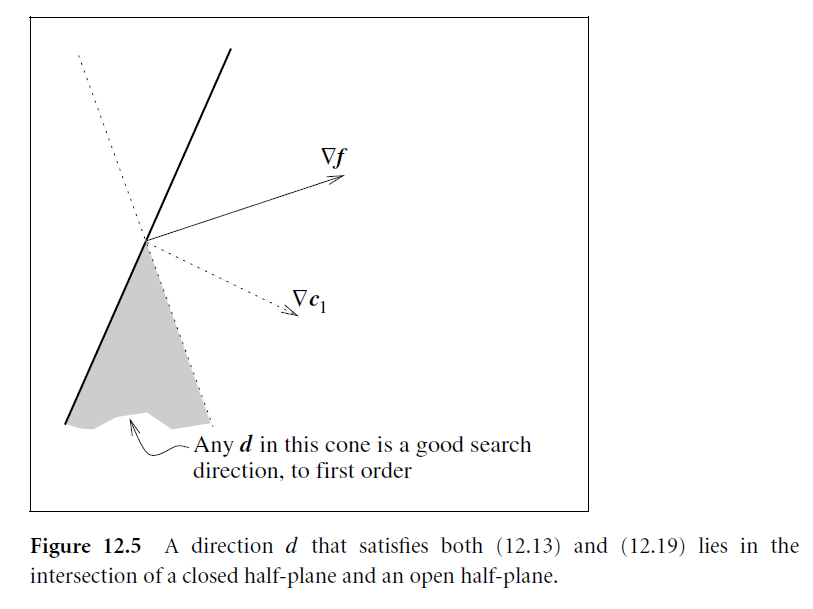
总结成拉格朗日函数形式：

$$\nabla \mathcal{L}(x^*,\lambda^*)=0,对于任意 \lambda \geq 0\\ \lambda^* c(x^*)=0$$

$\lambda^* c(x^*)=0$ 这也被称之为互补松弛条件：

当c(x)>0的时候（约束不起作用），$\lambda$ 为0，也就是说只需要满足$\nabla f(x)=0$ 这一个条件。

当c(x)=0的时候，约束发挥作用，类比于情况一，要满足两个条件。

情况3：两个不等号约束

$$\min x_1+x_2\\ s.t.2-x_1^2-x_2^2 \geq 0,\\ x_2 \geq 0$$

问题转化为一个半圆，如图所示：

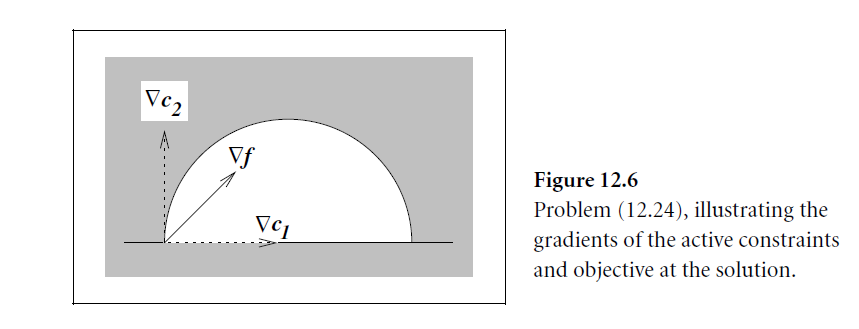
条件写为:

$$\nabla \mathcal{L}(x^*,\lambda^*)=0\\ \lambda^* \geq 0$$

互补松弛条件：

$$\lambda^* c(x^*)=0$$

找一些点进行检查： $x=(\sqrt 2,0)^T$，可以找到 $d=(-1,0)^T$

$x=(1,0)^T$，可以找到 $d=(-1/2,1/4)^T$

$x=(-\sqrt 2,0)^T$，满足条件，$\lambda^*=(1/2 \sqrt2,1)^T$, 是一个极值点。

一阶最优条件,KKT条件

定义拉格朗日函数： $$ \mathcal{L}(x, \lambda)=f(x)-\sum_{i \in \mathcal{E} \cup \mathcal{I}} \lambda_{i} c_{i}(x) $$ 一阶必要条件：