VAE模型——目前最流行的生成模型之一
本篇文章参考:《Tutorial on Variational Autoencoders》 CARL DOERSCH, Carnegie Mellon/ UC Berkeley
abstract
VAE是目前最流行的无监督学习模型之一。VAEs在生成复杂数据,比如手写数据集,房屋号,CIFAR图片、从部分图片预测完整图片领域取得了非常好的成绩。这篇教程介绍了VAE背后的机理,解释了后面的数学原理,描述了一些经验。
introduction
生成模型是一类机器学习模型,用于拟合P(X)。其中X是一个高维向量(张量),比如说图片。
生成模型的工作就是捕获X各个维度之间的关系,比如说:一个像素点的周围和它的颜色相同,是同一个对象。
如果说现在有数据集X,其实可以就算出P(X)的,对于图片来说,如果P(\text{图片})是一个很高的概率,说明它非常像真实图片。但是我们其实并不需要P(X),因为知道那种图片的出现概率大小并不能帮助我们合成它。
我们关心的问题是:生成更多与样本数据相似的数据而不是一模一样的数据。比如说:一张图片合成出一张从未见过的图片,一个手写数据合成出一个从未见过的手写数据。
用数学角度来说,这是一个这样的过程:我们从一个未知的分布P_{gt}(X)中采样得到X。我们想学习一个可以采样的模型P,这个P非常接近P_{gt}。
学习这个模型P,在机器学习社区早就被广泛研究了,有三个严重的缺点:
- 对于数据的结构有强假设;
- 做了多个近似,使得模型并不准确;
- 计算困难,比如依赖于MCMC。
现在鉴于深度学习的发展,通过反向传播可以得到一个强大的函数近似器。这个优势使得我们使用神经网络来构建生成模型。
目前最流行的深度生成模型是VAE,VAE的优势在于:1. 弱假设;2.可以通过反向传播快速训练;3. 在高容量的模型上,近似导致的误差理论上很小。
隐变量模型
训练一个生成模型的时候,各个维度之间的依赖关系越复杂,这个模型越难训练。比如说在生成数字的时候,做边生成了一半的5,右边生成了一半的0,这个生成图片就非常假。
自然地,在未生成任何像素点之前,有一个值决定生成哪个数字,这种决定被称为隐变量。帮助模型先决定要如何生成哪个类型的变量,称之为“隐变量”。比如说手写数据,在模型生成之前,首先给定隐变量 z=1,来使得模型生成满足这一类型,可以提高模型生成的准确性。
但是如果隐变量的维度太低,那么我们对事物的理解就过于片面了。那么现在说:有一个向量 z , 在一个高维度的空间 \mathcal{Z} 。同时我们有它的概率密度函数:
此时有一个判别方程 f ,它的参数为 \theta \in \Theta,可以将 z 生成到 X 的空间(\mathcal{X})上:
虽然 f 是确定的,但是 z 是一个随机变量,所以 f(z;\theta) 是一个在 \mathcal{X} 空间上的随机变量。
我们希望 f(z;\theta) 与 P(X) 相似, 这样的话我们可以通过采样 z 来在 f(z;\theta) \approx P(X) 中采样。
为了让整个过程的数学描述更加准确,我们将生成过程写为:
在这里 f(z;\theta) 被写为了 P(X \mid z ; \theta) 以便于准确描述 X 与 z 的依赖关系。根据最大似然的模型选择,我们希望最大化 P(X)。在VAE中,这个模型的输出为一个高斯分布,写为:
这个高斯分布的均值为 f(z;\theta) ,方差为单位矩阵与标量 \sigma 的乘积,\sigma 是一个超参数。这样做是为了让某些采样导致的结果与 X 并不是那么像。一般来说,特别是训练期间,模型生成的结果不会与某个 X 一模一样。通过使用高斯分布,使得我们可以用梯度下降, f(z;\theta) 来接近 X 来提升 P(X) 。如果说就直接 X = f(z;\theta),这样的 “近似” 就不复存在了。当然也不一定非要用高斯分布,其他的分布也同样适用,不过要采取不同的重参数话技巧。
变分自编码器
变分自编码器并不是按照编码器解码器的结构进行设计的,但是由于最终的训练目标中包含了一个编码器和解码器,所以组装成自编码器。
编码器的图模型如下所示:
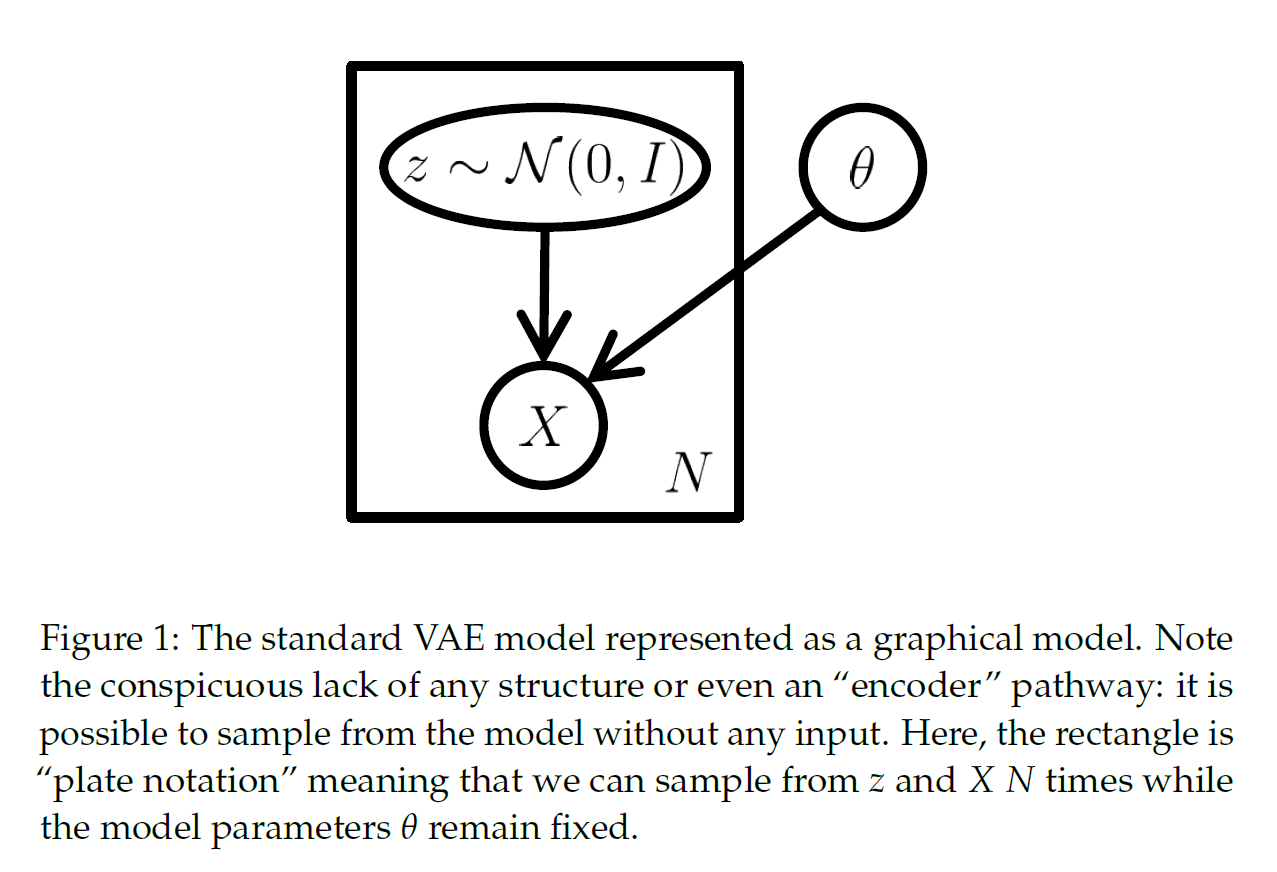
从图中可以发现,VAE并没有一个“encoder”,所以它可以任意采样。长方形和N的意思是我们可以从 z 或者 X 种采样N次,同时 \theta 是固定的。
前面提到了,最大化:
是VAE的目标。想要最大化这个 P(X) ,有两个问题需要解决:
- 我们要在什么样的 P(z) 中采样?
- 如果 P(z) 的维度太高,就必须采用蒙特卡罗方法,准确性怎么办?
如果采用有限个维度的z,那么模型的理解能力过于弱,我们想设计出一个具有更强理解力的模型,我们的P(z)需要是一个连续的,高维的分布。
在VAE中,z 从标准正态分布中采样:
有人会问:通过这样的简单的正态分布我们能采样到这么复杂的图片的分布吗?
事实上,任何分布都可以通过一个足够复杂的方程从正态分布转化过来,如图:
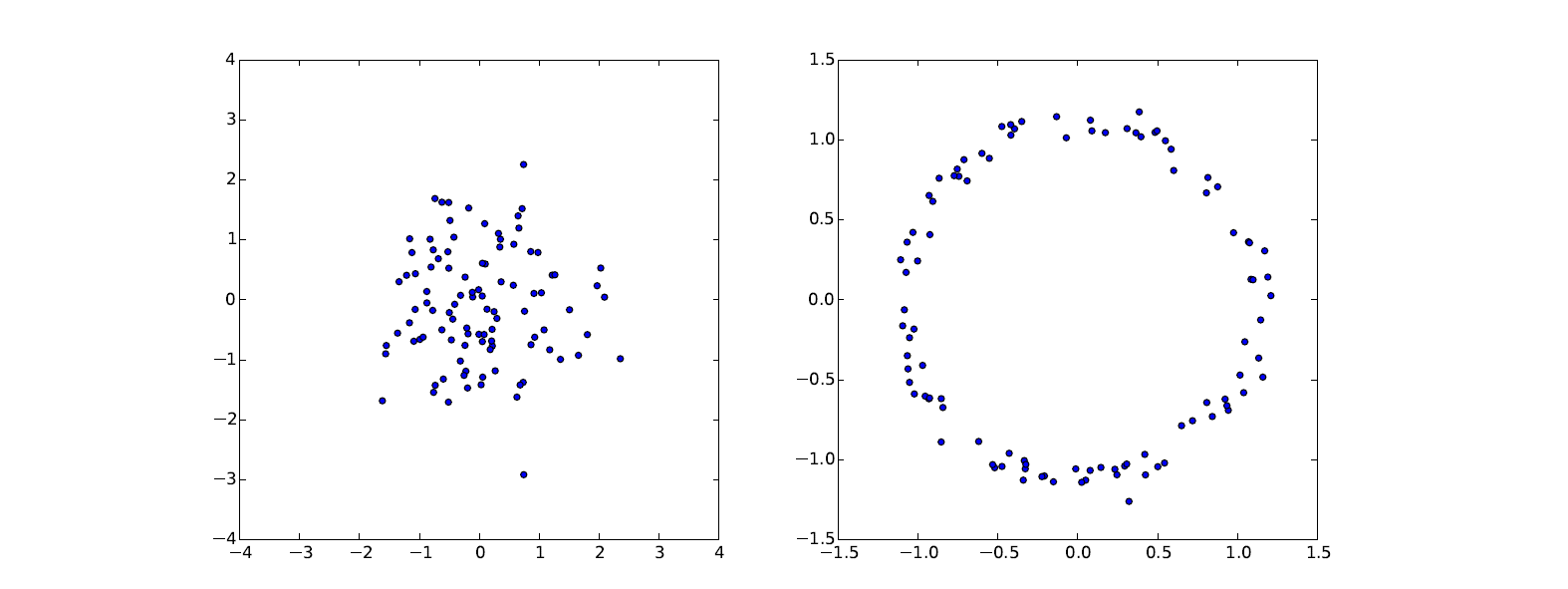
左图是从正态分布中的采样,通过一个函数(g(z)=z / 10+z /\|z\|)的变换我们得到了一个圆形分布。
所以我们需要的是一个强大的 g(z) ,并不需要过度关注先验分布 P(z) 。所以对于这样的概率分布:
只要f(z;\theta ) 足够强大, P(X \mid z ; \theta) 可以是任何分布。
现在我们的问题为:如何优化 P(X) ,使它的值达到最大?一般来说,我们希望构建出 P(X) 的表达式,并且能计算它的梯度,然后可以使用梯度算法对其进行优化。
传统的计算方式已经有了答案,采用蒙特卡罗方法采样 n 次,我们可以计算出:
但是由于维度太大,n 需要很大才能有效地估计出 P(X)。
建立目标
有没有办法:在采样的时候寻找一条捷径?事实上,P(X|z) 在很多 z 上是近乎等于0的,它对我们的采样并没有帮助。VAE的核心ideal就是构建一个新的函数Q,这个函数中采样出来的 z 对应的 P(X|z) 有值,以使得采样更加准确。也就是说:
这个 Q 满足两个条件:1. Q(z|X) 和 P(z|X) 非常相似。2. Q 中采样出来的 z 的分布空间要小于原来z 的先验空间。
为了满足第一个条件,我们写出 Q 与 P(z|X) 的KL散度:
最后写为:
这个表达式就是VAE的核心,我们需要最大化左边。
等号左边:
- P(X) 要尽量大。
- Q(z) 与 P(z|X) 的相似度要高,使得散度小。
等式右边:
右边是可计算的,所以使用梯度上升来优化右边的式子。写为:
这个式子使得VAE有了编码和解码的含义:Q 将 X 编码到z,P(X|z) 将 z 解码到X
优化目标
前面已经将优化目标确定:
其中:
在这里 $\mu, \Sigma, f $ 都是神经网络。最右侧的散度部分是可以借助两个正太分布的特点,直接计算出来的。假设两个正态分布\mathcal{N}\left(\mu_{0}, \Sigma_{0}\right) , \mathcal{N}\left(\mu_{1}, \Sigma_{1}\right):其散度计算依据下面的公式:
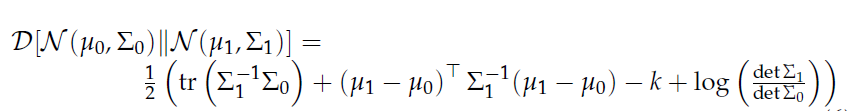
可以推广到高维空间:
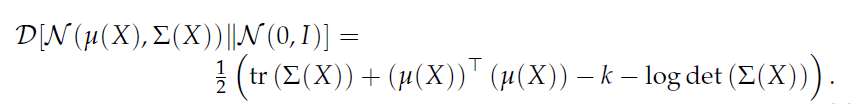
所以优化问题中的每一项都是可以计算的,那么我们使用SGD算法,从数据中采样出一个batch,X。
按照规则进行采样后,计算下式的梯度:
但是有一点要注意:如果按照正常的逻辑进行,计算图如下左图所示:
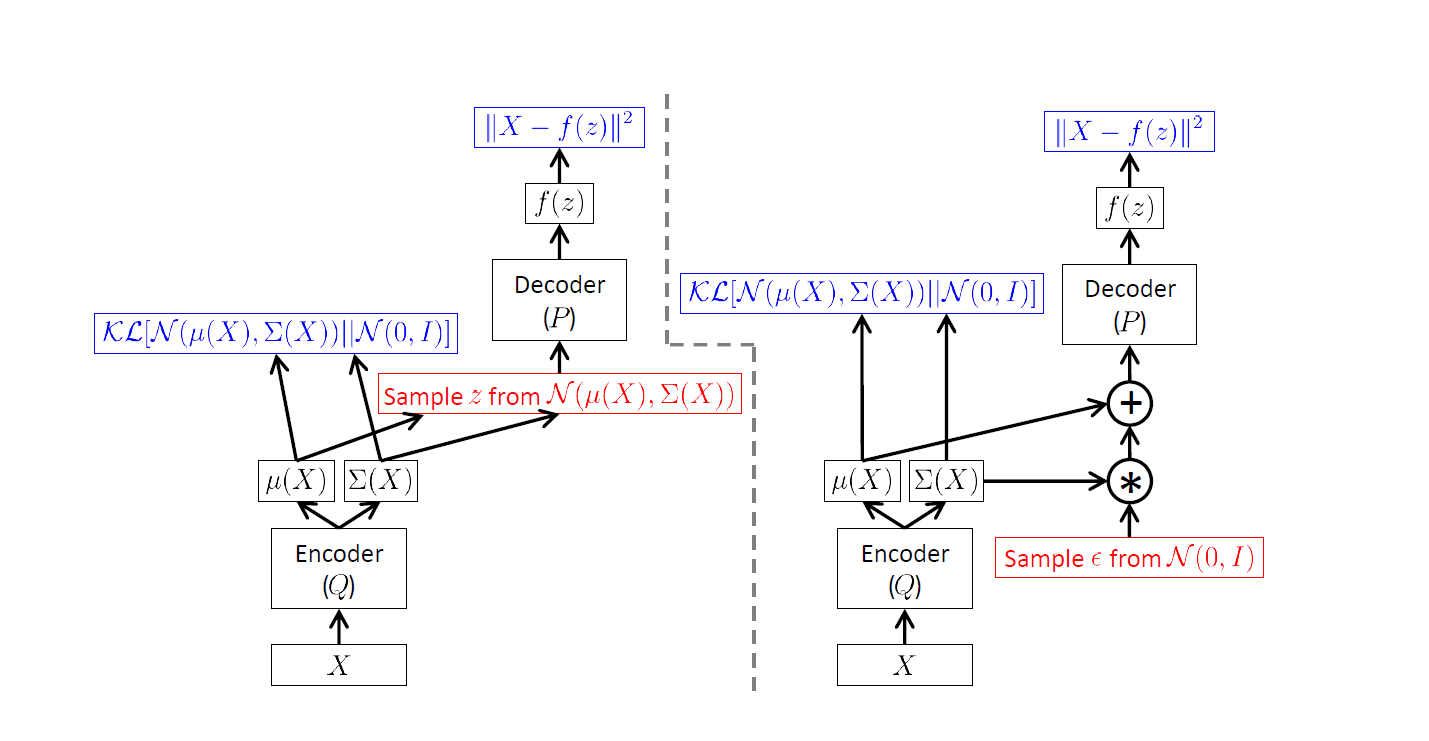
如果使用反向传播算法,那么梯度是无法传递到encoder的!期望的计算依赖于采样,散度的计算依赖于X,完全打断了与Q的联系。这样会导致梯度无法传播。如图所示:
通过重参数化技巧,让两个网络重新连接起来,使梯度能够传播。把模型改写为:
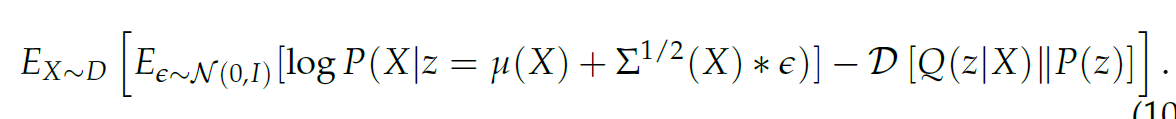
重参数化技巧就是为了从 \mathcal{N}(\mu(X), \Sigma(X)) 采样,我们首先在\epsilon \sim \mathcal{N}(0, I) 中采样,然后计算:z=\mu(X)+\Sigma^{1 / 2}(X) * \epsilon ,这等价于在 \mathcal{N}(\mu(X), \Sigma(X)) 中采样。
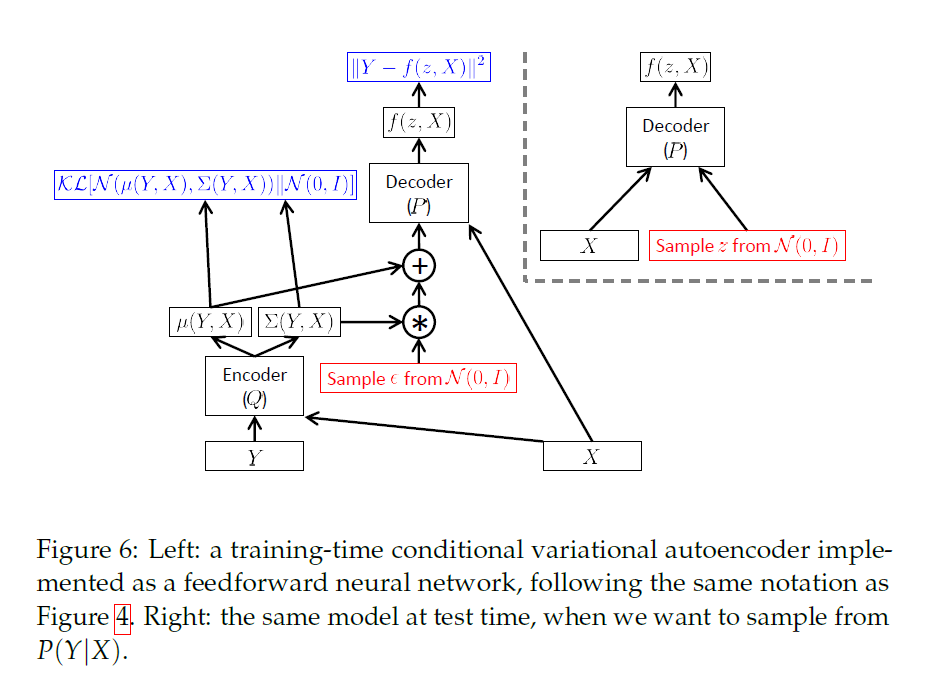
Conditional VAE
回到生成手写数据这个话题,我们不再考虑生成新的数字,我们在给定一部分笔迹的情况下复原整张图像。在计算机视觉领域被称之为hole filling。
这类问题的主要困难在于,这个输出是多模型的,对于下一个像素点填充方式有多种可能性。一个标准的回归模型在着这个情况下表现不佳,因为它会返回一个多个概率下的平均,一个“平均图片”显然不是一个好的结果。
我们需要这样的模型:给定一个图片,生成一个复杂的,多模型的分布来采样。CVAE通过修改上面的生成过程,都加上一个conditioning X,使得问题从输入-输出问题,改为输入一个,输出多个的问题。
原来生成模型定义为P(Y), 在conditioning的情况下,定义生成模型P(Y|X):
所以上面的推导写为: